impulse current. Electrical impulses and their parameters

electrical impulse, short-term change in electrical voltage or current. A short period of time is understood to be comparable to the duration transient processes in electrical circuits . I. e. are divided into high-voltage pulses, high current pulses, video pulses and radio pulses. I. e. high voltages are usually obtained when a capacitor is discharged to an active load and have an aperiodic form. Lightning discharges usually have the same form. Single I. e. similar shape with an amplitude of several sq. up to several MV with wave front 0.5-2 microsec and duration 10-10 -2 microsec used in testing electrical devices and equipment in high voltage technology. Current surges of great strength in form can be similar to I. e. high voltage (see Impulse technique high voltages).

Video pulses are called I. e. current or voltage (mainly of the same polarity) having a constant component other than zero. There are rectangular, sawtooth, trapezoidal, exponential, bell-shaped and other video pulses ( rice. one , a-d). Characteristic elements that determine the shape and quantitative parameters of the video pulse ( rice. 2 ) are the amplitude A, the front t f, the duration t i, the decline t s and the bevel of the top (D A), usually expressed in% of A. A periodic sequence of video pulses is characterized by a repetition frequency and duty cycle (the ratio of the repetition period to the duration of I. e.) . Duration of video pulses - from shares sec up to tenths ns (10 -9 sec). Video pulses are used in television, computer technology, radar, experimental physics, automation, etc.

Intermittent RF or microwave oscillations are called radio pulses. electric current or voltage ( rice. one , e), the amplitude and duration of which depend on the parameters of the modulating oscillations. The duration and amplitude of the radio pulses correspond to the parameters of the modulating video pulses; additional parameter - carrier frequency. Radio pulses are mainly used in radio engineering and communication technology. The duration of radio pulses is in the range of fractions sec before ns

Lit.: Itshoki Ya. S., Pulse devices, M., 1959; Fundamentals of impulse technology, M., 1966; Brammer Yu. A., Pashchuk I. N., Pulse technology, 2nd ed., M., 1968.

Great Soviet Encyclopedia M.: "Soviet Encyclopedia", 1969-1978

Under electrical impulse understand the deviation of voltage or current from a certain constant level (in particular, from zero), observed for a time less than or comparable to the duration of transients in the circuit.

As already mentioned, a transient process is understood as any abrupt change in the steady state in an electrical circuit due to the action of external signals or switching within the circuit itself. Thus, the transient process is the process of transition of an electric circuit from one stationary state to another. No matter how short this transitional process is, it is always finite in time. For circuits in which the time of existence of the transient process is incomparably less than the time of the external signal (voltage or current), the operating mode is considered to be steady, and the external signal itself for such a circuit is not pulsed. An example of this is the operation of an electromagnetic relay.

When the duration of the voltage or current signals acting in the electrical circuit becomes commensurate with the duration of the establishment processes, the transient process has such strong influence on the form and parameters of these signals, that they cannot be ignored. In this case, most of the time the signal affects the electrical circuit coincides with the time of existence of the transient process (Fig. 1.4). The mode of operation of the circuit during the action of such a signal will be non-stationary, and its effect on the electrical circuit will be pulsed.

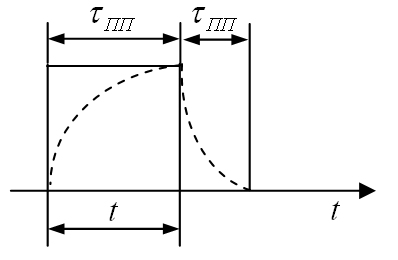
Fig.1.4. Relationship between signal duration and duration

transition process:

a) the duration of the transient process is much less than the duration

signal ( τ pp<< t );

b) the duration of the transient process is commensurate with the duration

signal ( τ pp ≈ t ).

It follows that the concept of an impulse is associated with the parameters of a particular circuit and that not for any circuit a signal can be considered impulse.

In this way, An electrical impulse for a given circuit is a voltage or current acting for a period of time commensurate with the duration of the transient process in this circuit. In this case, it is assumed that there should be a sufficient time interval between two consecutive pulses in the circuit, exceeding the duration of the establishment process. Otherwise, signals of complex shape will appear instead of pulses (Fig. 1.5).

Fig.1.5. Complex shape electrical signals

The presence of time intervals gives the pulse signal a characteristic discontinuous structure. Some conventionality of such definitions lies in the fact that the process of establishment theoretically lasts indefinitely.

There may be such intermediate cases when the transient processes in the circuits do not have time to practically end from pulse to pulse, although the operating signals continue to be called pulsed. In such cases, there are additional distortions in the shape of the pulses caused by the superposition of the transient process on the beginning of the next pulse.

There are two types of impulses: video pulses and radio pulses . Video pulses are obtained when switching (switching) the DC circuit. Such pulses do not contain high-frequency oscillations and have a constant component (average value) that is different from zero.

Video pulses are usually distinguished by their shape. On fig. 1.6. the most common video pulses are shown.

Rice. 1.6. Forms of video pulses:

a) rectangular; b) trapezoidal; v) pointed;

G) sawtooth; e) triangular; e) bipolar.

Consider the main parameters of a single pulse (Fig. 1.7).

Rice. 1.7. Single pulse parameters

The shape of the pulses and the properties of its individual sections are quantitatively evaluated by the following parameters:

· Um is the amplitude (maximum value) of the pulse. Pulse amplitude U m (I m) expressed in volts (amps).

· τ and - pulse duration. Usually, measurements of the duration of impulses or individual sections are made at a certain level from their base. If this is not specified, then the pulse duration is determined at the zero level. However, most often the pulse duration is determined at the level 0.1U m or 0.5U m counting from the base. In the latter case, the pulse duration is called active duration and denoted τ ia . If necessary, and depending on the shape of the pulses, the accepted values ​​of the levels for measurement are specially stipulated.

· τ f is the rise time, determined by the rise time of the pulse from the level 0.1U m to level 0.9U m .

· τ s is the duration of the cutoff (trailing edge), determined by the time of the decay of the pulse from the level 0.9U m to level 0.1U m . When the rise or fall time is measured at the level 0.5U m , it is called the active duration and is denoted by adding the index "a" similar to active pulse width. Usually τ f and τ s is a few percent of the pulse duration. The less τ f and τ s compared with τ and , the more the pulse shape approaches a rectangular one. Sometimes instead τ f and τ s the fronts of the pulse characterize the rate of rise (fall). This value is called steepness (S) of the front (cutoff) and expressed in volts per second (V/With) or kilovolts per second (kV/With) . For a square wave

………………………………(1.14).

· The segment of momentum between the fronts is called a flat top. Figure 1.7 shows the decline of a flat top (ΔU) .

· Power in an impulse. Energy W The pulse divided by its duration determines the power in the pulse:

………………………………(1.15).

It is expressed in watts. (W) , kilowatts (kW) or flat units

zah watt.

Pulse devices use pulses that have durations from fractions of a second to nanoseconds. (10 - 9 s) .

The characteristic sections of the pulse (Fig. 1.8), which determine its shape,

are:

front (1 - 2);

top (2 - 3);

slice (3 - 4), sometimes called the trailing edge;

tail (4 - 5).

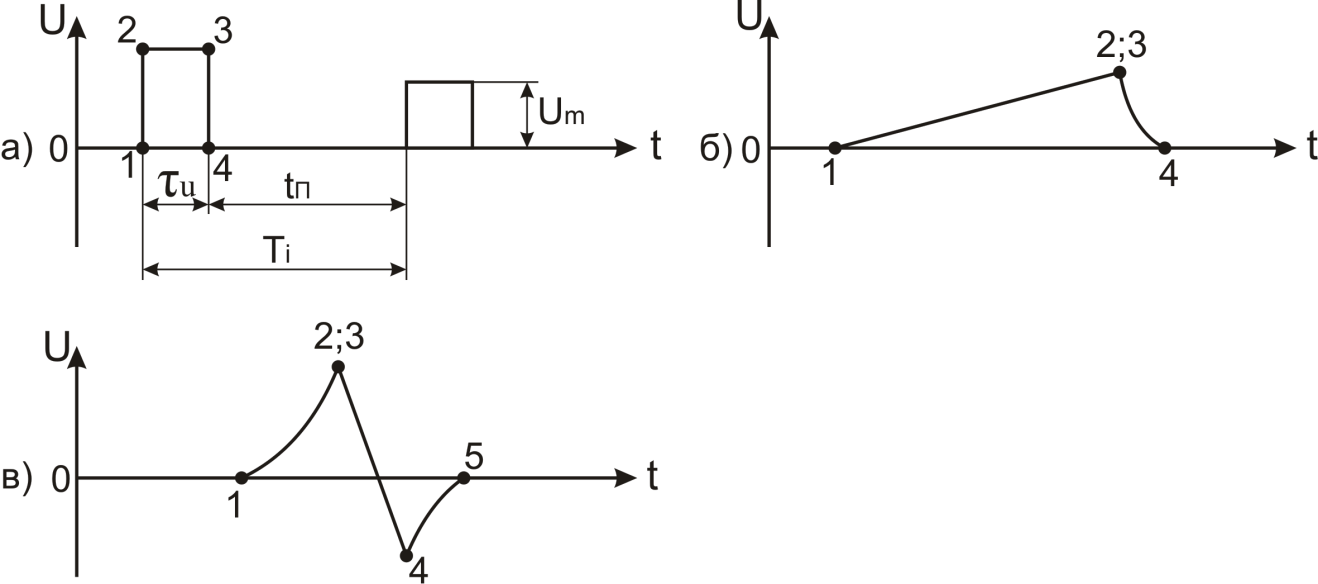
Fig.1.8. Characteristic sections of the pulse

Individual sections of pulses of various shapes may be absent. It should be borne in mind that real pulses do not have a shape strictly corresponding to the name. Distinguish pulses of positive and negative polarity, as well as bilateral (opposite) pulses

(Fig. 1.6, e).

Radio pulses are pulses of high-frequency voltage or current oscillations, usually of a sinusoidal shape. Radio pulses do not have a constant component. Radio pulses are obtained by modulating high-frequency sinusoidal oscillations in amplitude. In this case, amplitude modulation is performed according to the law of the control video pulse. The shapes of the corresponding radio pulses obtained using amplitude modulation are shown in Figs. 1.9:

Fig.1.9. Forms of radio pulses

Electrical impulses that follow each other at regular intervals are called periodic sequence (Fig.1.10).

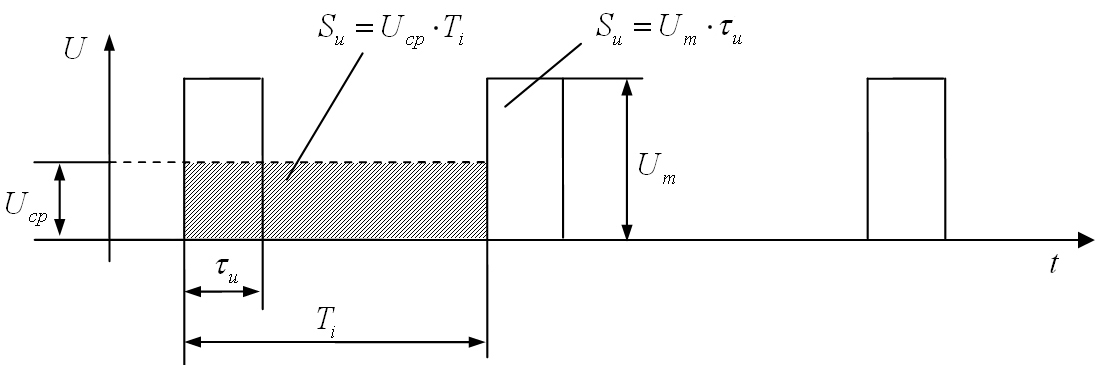
Fig.1.10. Periodic pulse train

The periodic sequence of pulses is characterized by the following parameters:

・Recurrence period T i is the time interval between the beginning of two adjacent unipolar pulses. It is expressed in seconds (With) or sub-seconds (ms; µs; ns). The reciprocal of the repetition period is called the frequency of repetition (following) of pulses. It defines the number of pulses in one second and is expressed in Hertz. (Hz) , kilohertz (kHz) etc.

……………………………….. (1.16)

· Duty cycle of a sequence of pulses is the ratio of the repetition period to the duration of the pulse. Denoted by letter q :

………………… (1.17)

The duty cycle is a dimensionless quantity that can vary over a very wide range, since the duration of the pulses can be hundreds or even thousands of times less than the pulse period or, conversely, occupy most of the period.

The reciprocal of the duty cycle is called the duty cycle. This value is dimensionless, less than unity. It is marked with the letter γ :

…………………………(1.18)

Pulse sequence with q = 2 called "meander" . Such

sequences (fig.1.6, e). If T i >> τ and , then such a sequence is called radar.

· The average value (constant component) of the impulse fluctuation. When determining the average value of the impulse fluctuation for the period U cf (or I cf) the voltage or current impulse is distributed evenly over the entire period so that the area U cf T i was equal to the area of ​​the impulse S and = U m τ and (Fig. 1.10).

For pulses of any shape, the average value is determined from the expression

……………………(1.19),

where U(t) is an analytical expression for the pulse shape.

For a periodic pulse train rectangular shape, in which U(t) = Um , repetition period T i and pulse duration τ and , this expression after substitution and transformation takes the form:

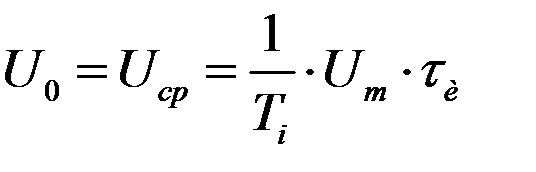…………………….(1.20).

From fig. 1.10 shows that S and = U m τ and = U cf T i , from which follows:

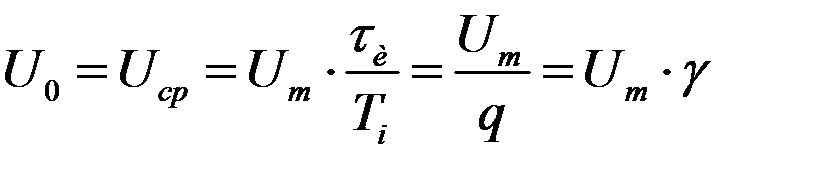……………(1.21),

where U 0 is called the constant component.

Thus, the average value (DC component) of the voltage (current) of a sequence of rectangular pulses in q times smaller than the pulse amplitude.

· Average power of the pulse train. Pulse energy W , related to the period T i , determines the average pulse power

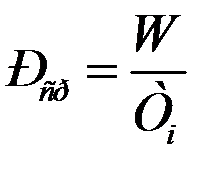…………………………….. (1.22).

Comparing Expressions R and and R cf , we get

R and τ i = R cf T i ,

whence it follows

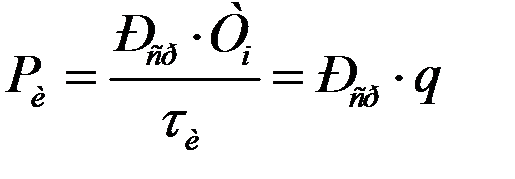…………………(1.23)

and

……………………. (1.24),

those. average power and power per pulse differ in q once.

It follows that the pulse power provided by the generator can q times the average power of the generator.

Tasks and exercises

1. The pulse amplitude is 11 kV, the pulse duration is 1 μs. Determine the steepness of the pulse front, if we consider the front duration equal to 20% of the pulse duration.

2. The amplitude of rectangular pulses with a repetition rate of 1250 Hz and a duty cycle of 2300 is 11 kV. Determine the steepness of the rise and fall, if we consider the duration of the rise and fall equal to 20% of the pulse duration.

3. Determine the time constant of the circuit consisting of a capacitor with a capacity of 5000 pF and an active resistance of 0.5 MΩ.

4. Determine the time constant of the circuit, consisting of an inductance of 20 mH and a resistance of 5 kΩ.

5. Determine the average power of the radio transmitter of the radar, which has the following parameters: pulse power 800 kW; probing pulse duration 3.2 μs; the repetition rate of probing pulses is 375 Hz.

6. A 400 pF capacitor is charged from a 200 V DC voltage source through a 0.5 MΩ resistance. Determine the voltage across the capacitor 600 µs after the start of the charge.

7. A DC source with a voltage of 50 V is connected to a circuit consisting of a capacitor with a capacity of 10 pF and a resistance of 2 MΩ. Determine the current at the moment of switching on and 40 μs after switching on.

8. A capacitor charged to a voltage of 300 V is discharged through a resistance of 300 MΩ. Determine the magnitude of the discharge current through time t = 3τ after the start of the discharge.

9. What time will it take to charge a 100 pF capacitor to a voltage of 340 V if the source voltage is 540 V and the charge circuit resistance is 100 kOhm?

10. A circuit consisting of an inductance of 10 mH and a resistance of 5 kΩ is connected to a constant voltage source of 250 V. Determine the current flowing in the circuit 4 µs after switching on.

Chapter 2

Linear and non-linear circuits

In impulse technology, circuits and devices are widely used that generate voltages of one form from the voltage of another. Such problems are solved with the help of linear and non-linear elements.

An element whose parameters (resistance, inductance, capacitance) do not depend on the magnitude and direction of currents and applied voltages is called linear. Circuits containing linear elements are called

linear.

Properties of linear circuits:

· The current-voltage characteristic (VAC) of a linear circuit is a straight line, i.e. the values ​​of currents and voltages will be interconnected by linear equations with constant coefficients. An example of a CVC of this kind is Ohm's law: .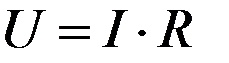

· For the calculation (analysis) and synthesis of linear circuits, the principle of superposition (overlay) is applicable. The meaning of the superposition principle is as follows: if a sinusoidal voltage is applied to the input of a linear circuit, then the voltage on any of its elements will have the same shape. If the input voltage is a complex signal (that is, it is the sum of harmonics), then all harmonic components of this signal are preserved on any element of the linear circuit: in other words, the shape of the voltage applied to the input is preserved. In this case, only the ratio of harmonic amplitudes will change at the output of the linear circuit.

· A linear circuit does not transform the spectrum of the electrical signal. It can change the components of the spectrum only in amplitude and phase. This is the cause of linear distortion .

· Any real linear circuit distorts the waveform due to transients and finite bandwidth.

Strictly speaking, all elements of electrical circuits are non-linear. However, in a certain range of variable values, the nonlinearity of the elements manifests itself so little that it can practically be neglected. An example is a radio frequency amplifier (URCH) of a radio receiver, to the input of which a signal of a very small amplitude is fed from the antenna.

The non-linearity of the input characteristic of the transistor in the first stage of the URF is so small within a few microvolts that it is simply not taken into account.

Usually, the area of ​​non-linear behavior of an element is limited, and the transition to non-linearity can occur either gradually or abruptly.

If a complex signal is applied to the input of a linear circuit, which is the sum of harmonics of different frequencies, and the linear circuit contains a frequency-dependent element ( L or C ), then the shape of the voltages on its elements will not repeat the shape of the input voltage. This is because the harmonics of the input voltage are passed differently by such a circuit. As a result of the passage of the input signal through the capacitances and inductances of the circuit, the ratios between the harmonic components on the circuit elements change in amplitude and phase with respect to the input signal. As a result, the ratios between the amplitudes and phases of the harmonics at the input of the circuit and at its output are not the same. This property is the basis for the formation of pulses using linear circuits.

An element whose parameters depend on the magnitude and polarity of the applied voltages or currents flowing is called non-linear , and a chain containing such elements is called non-linear .

Nonlinear elements include electrovacuum devices (EVD), semiconductor devices (SPP) operating in the nonlinear section of the current-voltage characteristic, diodes (vacuum and semiconductor), as well as transformers with ferromagnets.

Properties of non-linear circuits:

· The current flowing through a non-linear element is not proportional to the voltage applied to it, i.e. the relationship between voltage and current (VAC) is non-linear. An example of such a CVC is the input and output characteristics of EVP and PPP.

Processes occurring in nonlinear circuits are described by nonlinear equations different kind, whose coefficients depend on the voltage (current) function itself or on its derivatives, and the CVC of a nonlinear circuit has the form of a curve or a broken line. An example is the characteristics of diodes, triodes, thyristors, zener diodes, etc.

· For non-linear circuits the principle of superpositions is inapplicable. When an external signal is applied to nonlinear circuits, currents always appear in them, containing new frequency components that were not in the input signal. This is the cause of

non-linear distortion , resulting in a non-linear output signal

circuit is always different in shape from the input signal.

Differentiating circuits

To get momentum desired shape from a given form of voltage using a passive electrical circuit, it is necessary to know the forming properties of this circuit. Forming properties characterize the ability of a linear circuit to change the shape of the transmitted (processed) signal in a certain way and are completely determined by the type of its frequency and time s x characteristics.

In pulse technology, linear two- and four-terminal networks are widely used to form signals.

differentiating A circuit is called, at the output of which the voltage is proportional to the first derivative of the input voltage. Mathematically, this is expressed by the following formula:

………………………. (2.1),

where U in - voltage at the input of the differentiating circuit;

U out- voltage at the output of the differentiating circuit;

k - coefficient of proportionality.

Differentiating circuits (DC) are used to differentiate video pulses. In this case, differentiating circuits allow the following transformations:

shortening of rectangular video pulses and formation of pointed pulses from them, which serve to trigger and synchronize various pulse devices;

Obtaining time derivatives of complex functions. This is used in measuring technology, auto-regulation and auto-tracking systems;

Formation of rectangular pulses from sawtooth ones.

The simplest differentiating circuits are capacitive ( RC ) and inductive ( RL ) chains (fig.2.1):

Fig.2.1. Types of differentiating circuits:

a) capacitive DC; b) inductive DC

Let us show that RC - the chain under certain conditions becomes differentiating.

It is known that the current flowing through the capacitance is determined by the expression:

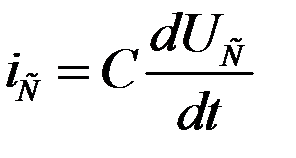........................................... (2.2).

At the same time, from Fig. 2.1, a it's obvious that

,

because R and C are a voltage divider. Because the voltage

, then .

Output voltage

………………….... (2.3).

Substituting expression (2.2) into (2.3), we obtain:

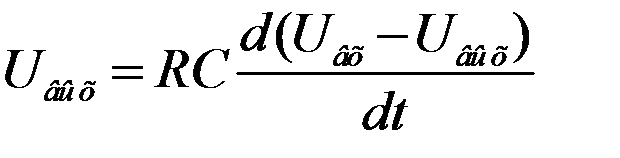……………… (2.4).

If we choose a sufficiently small value R so that the condition

then we get the approximate equality

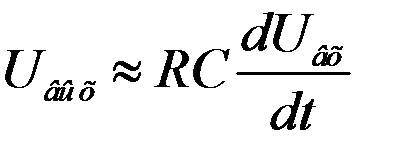……………………….. (2.5).

This equality is identical to (2.1).

Select R a sufficiently small value - this means ensuring the fulfillment of the inequality

where ω in = 2πf in is the upper limiting frequency of the harmonics of the output signal, which still has significant for the shape of the output pulse.

Proportionality factor in expression (2.1) k = RC = τ is called time constant differentiating circuit. The more sharply the input voltage changes, the smaller the value τ must have a differentiating circuit so that the output voltage is close in shape to the derivative of U in . Parameter τ=RC has the dimension of time. This can be confirmed by the fact that, in accordance with the International System of Units (SI), the unit of electrical resistance is

,

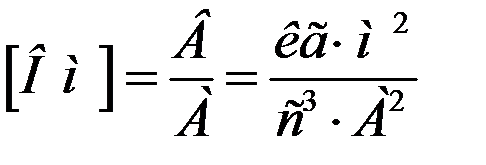and the unit of measurement of electric capacitance

.

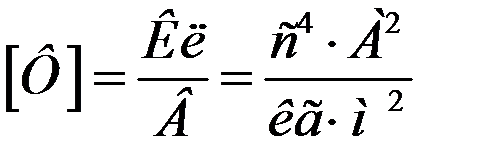Hence,

The principle of operation of the differentiating circuit.

A schematic diagram of a capacitive differentiating circuit is shown in Fig. 2.2, and voltage diagrams are shown in Fig. 2.3.

Fig.2.2. Schematic diagram of a capacitive differentiating circuit

Let an ideal rectangular pulse be fed to the input, for which

τ f = τ s = 0, a internal resistance signal source R i = 0 .Let the momentum be determined by the following expression:

1. The initial state of the circuit (t< t 1).

In original state U in = 0; U c = 0; i s = 0; U out = 0.

1. First power surge (t = t 1).

At the time t \u003d t 1, a voltage jump is applied to the DC input

U in = E. In this moment U c \u003d 0 , because for an infinitely small period of time, the capacity cannot be charged. But, in accordance with the switching law, the current through the capacitance can increase instantly. Therefore, at the moment t \u003d t 1, the current flowing through the capacitance will be equal to

Therefore, the voltage at the output of the circuit at this moment will be equal to

1. Capacitor charge (t 1< t < t 2).

After the jump, the charge of the capacitor begins with a current decreasing according to an exponential law:

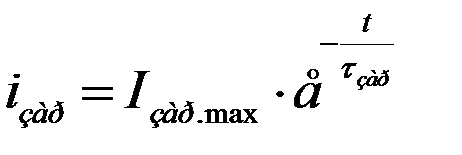
Fig.2.3. Plots of voltages on the elements of the differentiating circuit

The voltage across the capacitor will rise exponentially

…………………… (2.6).

The DC output voltage will drop as the voltage rises.

charge on the capacitor, because R and C are a voltage divider:

…………. (2.7).

It must be remembered that at any time for the voltage divider, the equality

whence it follows that

which confirms the validity of expression (2.7).

Theoretically, the charge of the capacitor will continue indefinitely, but in practice this transient process ends after

(3…5)τ charge = (3…5)RC .

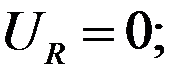
1. The end of the capacitor charge (t \u003d t 2).

After the end of the transient process, the capacitor charge current becomes zero. Therefore, the voltage at the output of the differentiating circuit

reaches almost zero value, i.e. at time t = t 2

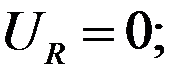
1. Steady state (t 2< t < t 3).

Wherein

1. Second voltage jump (t = t 3).

At the point in time t = t3 the voltage at the input of the differentiating circuit abruptly drops to zero. Capacitor C becomes a source of tension, tk. it is charged to the point .

Since, in accordance with the switching law, the voltage across the capacitor cannot change abruptly, and the current flowing through the capacitance can change abruptly, then at the moment t = t3 the output voltage drops abruptly to – E . In this case, the discharge current in this moment time becomes maximum:

,

and the voltage at the output of the differentiating circuit

.

The output voltage has a minus sign, because current has changed direction.

1. Capacitor discharge (t 3< t < t 4).

After the second jump, the voltage across the capacitor begins to decrease exponentially:

;

;

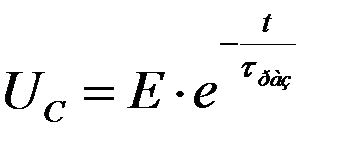1. The end of the capacitor discharge and the restoration of the initial state of the circuit (t≥ t4).

After the end of the transient discharge of the capacitor

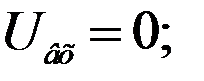
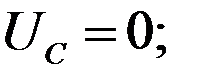
Thus, the circuit returned to its original state. The end of the capacitor discharge occurs almost at t = (3…5)τ = (3…5) RC.

Since we have taken the internal resistance of the signal source R i = 0, then we can assume that the time constants of the charge and discharge circuits of the capacitor τ charge = τ times = τ =RC .

In such an ideal circuit, the amplitude of the output voltage U out. m ah does not depend on the value of the circuit parameters R and C , and the duration of the pulses at the output is determined by the value of the time constant of the circuit τ=RC . The smaller the value R and C , the faster the transient processes of charge and discharge of the capacitance end, the shorter the pulse at the output of the circuit.

Theoretically, the duration of the pulse at the output of the differentiating circuit, determined by the base, turns out to be infinitely long, since the voltage at the output falls off exponentially. Therefore, the pulse duration is determined at a certain level from the base

U 0 = αU out (fig.2.4):

Fig.2.4. Determining the pulse duration at the level U 0 after

differentiation

Let us determine the duration of the differentiated pulse at the level

U 0 = αU out :

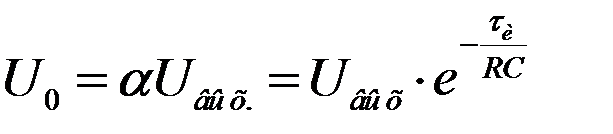………………. (2.8),

where 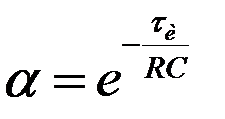and ……………………… (2.9).

Differentiation is always accompanied by a shortening of the pulse duration. This means that the capacity C should have time to fully charge during the current input differentiable pulse. Therefore, the condition for practical differentiation in order to shorten the pulse duration is the ratio:

τ and in > 5τ = 5RC.

The less τ circuit, the faster the capacitor charges and discharges and the shorter the duration of the output pulses, the more pointed they become and, therefore, the more accurate the differentiation. However, reduce τ appropriate up to a certain limit.

The change in the shape of the pulse at the output of the differentiating circuit can be explained in terms of spectral analysis.

Each harmonic of the input pulse is divided between R and C . For harmonics low frequencies, which determine the top of the input pulse, the capacitor represents a large resistance, because

>> R .

Therefore, the flat top of the input pulse is almost not transmitted to the output.

For the high-frequency components of the input pulse, which form its front and cut,

<< R .

Therefore, the front and edge of the input pulse are transmitted to the output almost without attenuation. These considerations allow us to define the differentiating chain as high pass filter .

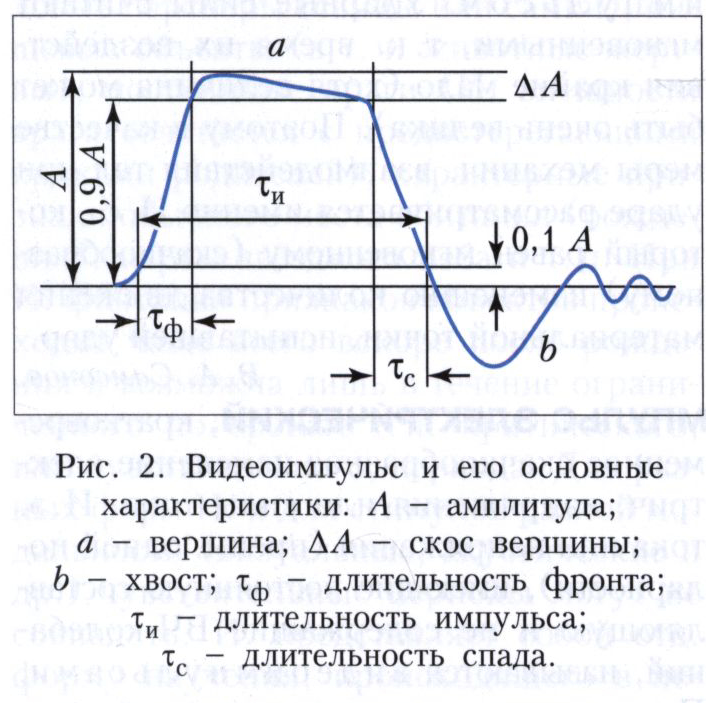
ELECTRIC PULSE, a short-term abrupt change in electrical voltage or current. A pulse of electric current or voltage (mainly of the same polarity), having a constant component and not containing RF oscillations, are called video pulses. According to the nature of the change in time, video pulses of rectangular, sawtooth, trapezoidal, bell-shaped, exponential and other shapes are distinguished (Fig. 1, a-d). A real video pulse can have a rather complex shape (Fig. 2), which is characterized by amplitude A, duration τ I (counted at a predetermined level, for example, 0.1 A or 0.5 A), rise time τ F and decay τ C (counted between 0.1 A and 0.9 A), peak bevel ΔA (expressed as a percentage of A). Rectangular video pulses are most widely used, on the basis of which synchronization, control and information signals are formed in computer technology, radar, television, digital transmission and information processing systems, etc. Sawtooth and exponential video pulses are used, for example, in scanning systems for televisions, radar indicators, oscilloscopes , as well as in the formation of complex radar signals with intra-pulse frequency modulation. The duration of video pulses ranges from fractions of a second to tenths of a nanosecond.

In addition to single and irregularly following in time streams of electrical impulses, periodic sequences are used in practice, which are additionally characterized by a period T or a repetition frequency f=T -1 . An important parameter of a periodic sequence of electrical impulses is the duty cycle (the ratio of the repetition period of impulses to their duration). According to the frequency distribution, electrical impulses are characterized by a spectrum, which is obtained by expanding the time function expressing the electric impulse in a Fourier series (for a periodic sequence of identical impulses) or a Fourier integral (for single impulses).

Electric pulses, which are time-limited (intermittent) HF or microwave oscillations, the envelope of which has the form of a video pulse (Fig. 1, e), are called radio pulses. The duration and amplitude of the radio pulses correspond to the parameters of the modulating video pulses; an additional parameter is the carrier frequency. Radio pulses are mainly used in radio and communication devices; their duration ranges from fractions of a second to several nanoseconds.

Lit .: Erofeev Yu. N. Pulse devices. 3rd ed. M., 1989; Brammer Yu. A., Pashchuk IN Impulse technology. M., 2005.

A typical example of rectangular pulses are primary telegraph and data signals, also called direct current pulses. They have the form of sequences of two- or unipolar rectangular pulses (Fig. 6.1, a).

Let us find the spectrum of a periodic sequence of unipolar pulses with period and amplitude UQ. Such a sequence can be represented as a Fourier series:

where is the circular repetition frequency or the first harmonic (spectral component) of the signal

Rice. 6.1 Pulse sequence (a) and its spectrum (b)

The coefficients determine the so-called spectrum of amplitudes, and the spectrum of phases. Wherein

where is the duty cycle of the pulse sequence. The constant component or the average value of the signal over the period. The spectrum of amplitudes for the case is shown in fig.

The spectrum of a periodic sequence of unipolar pulses at contains, in addition to the constant component, components with frequencies, etc. The difference between these spectral components (With increasing T decreases, while the components themselves also decrease in amplitude. At , the signal becomes non-periodic, and the spectrum becomes continuous. Instead of the concept of the amplitude spectrum, the concept of spectral density is introduced.Spectral density is defined as the ratio of the "amplitude of the spectral component" to an infinitely small frequency band and is calculated through the Fourier integral:

where is the spectral density of the amplitudes; - phase spectrum.

Knowing can be found using the inverse Fourier transform:

The spectral density of the amplitudes of a single rectangular pulse, up to a factor, is shown by the dashed line in Fig.

The spectrum of a periodic sequence of pulses and a single pulse contains components with a frequency from 0 to infinity, i.e., it is infinite. If a sequence of rectangular pulses is transmitted over a communication channel that always passes only a limited spectrum, then the waveform at the output of the channel changes. The waveform can be determined using the inverse Fourier transform (6.6).

In practice, the width of the signal spectrum is usually understood as the frequency range in which the main energy of the signal is concentrated. In this case, the concept of the effective width of the signal spectrum is introduced. On fig. - this is the frequency range from 0 to where about 90% of the signal energy is concentrated. This means that the shorter the pulse duration (the higher the telegraphy speed), the wider the spectrum. In particular, an infinitely short pulse has an infinitely extended spectrum with a uniform density. Thus, higher speed transmission requires higher bandwidth channels.

For a given duration of a single element, then the spectrum of the transmitted signal is influenced by two factors. One is the pulse shape, which must be carefully chosen to obtain a good (compact) signal spectrum. Another factor is the nature of the transmitted digital sequence, i.e. the spectrum depends on the statistical characteristics of the transmitted sequence, and the spectrum can be changed by recoding it.

To evaluate the distortion of DC pulses caused by spectrum clipping, consider the passage of a pulse through an ideal low-pass filter (LPF). As an input action, we use the step function

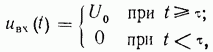
presented graphically in fig. 6.2. The choice of such an input action is due to the fact that, firstly, its use simplifies mathematical calculations, and secondly, a single rectangular pulse of finite duration can be represented as a sequence of two single voltage jumps of the opposite sign, shifted in time by an amount equal to the pulse duration (Fig. .6.3).

Rice. 6.2 Step function

Rice. 6.3. Representation of a single pulse

Rice. 6.4. Characteristics of an ideal low-pass filter

And, finally, knowing the characteristics of the process that is being established under the influence of a single jump, using the convolution theorem, one can find the process that is being established for an arbitrary form of action .

Let the input of an ideal low-pass filter with a cutoff frequency have the amplitude and phase-frequency characteristics of which have the form (Fig. 6.4):

where is the group time of the filter passage, at the moment the signal (6.7) is applied, which can be represented in the form

To obtain a signal at the output of the low-pass filter, we multiply all the components of the input signal by the modulus of the filter gain and subtract the phase shift at each frequency from the sine argument:

Substituting in (6.9) the value of the transfer coefficient from (6.8), we obtain